nlp_intro

3. Evaluation, data splits

Explanations and formulas:

• Eisenstein 3.2.3, 4.4 (ignore significance), 6.4.2
• Jurafsky-Martin 3.7, 4.7, 16.5

 

1. Data splits

 

 

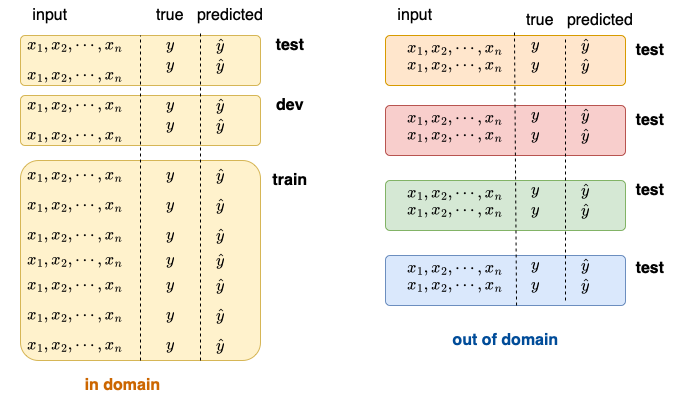
2. Comparing two sets of labels (confusion matrix)

• This evaluation is common in machine learning in general
• Measures: precision, recall, F-score, accuracy
• All except accuracy are calculated on binary decisions per label and need to be averaged
• In NLP, we use this kind of evaluation for tasks where we have a single label for a whole sentence, e.g. sentient analysis, similarity, inference, text classification

 

3. Comparing two sequences of labels

We have to take into account the order of the labels. The true sequence of labels is called reference.

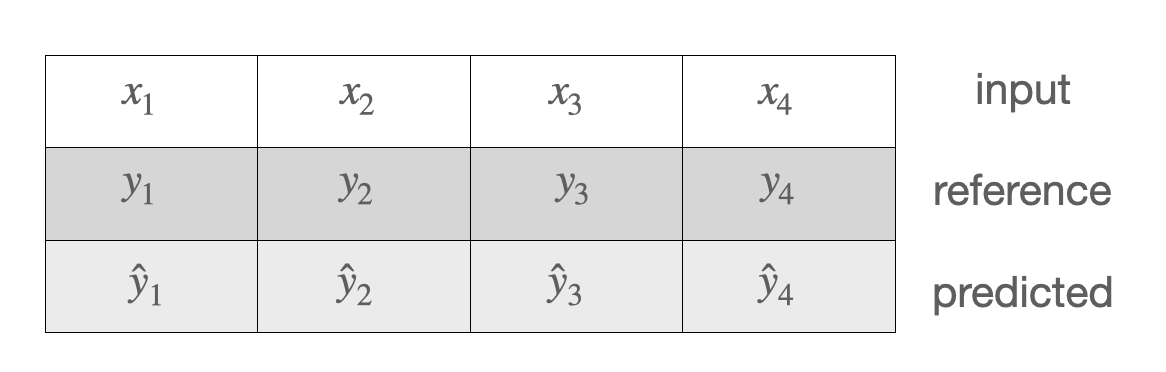
Measures:

• WER mostly in speech to text conversion
• BLEU mostly in machine translation
• chrF starting to be used more than BLEU in machine translation

 

4. Comparing a sequence of labels to a model

We can evaluate a sequence against a model. For this, we rely on information theory, specifically:

• Entropy
• Cross-entropy
• Perplexity

These quantities are used as measures of the quality of generated text, but also (and much more!) as loss functions in training.

 

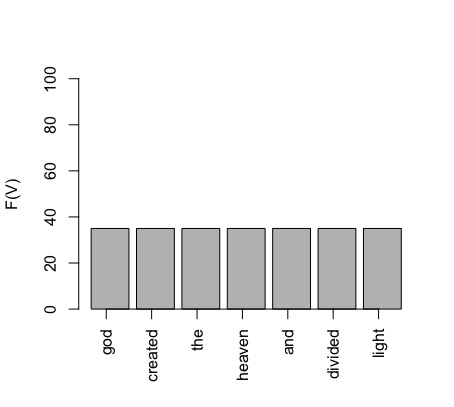
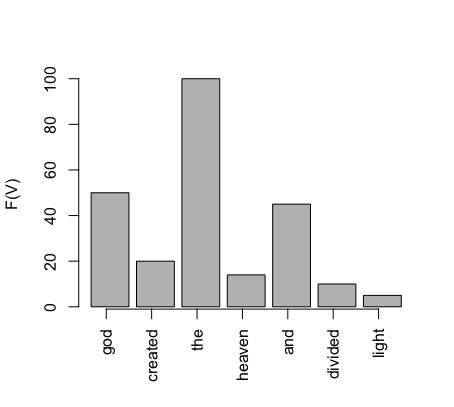
E.g. high vs. low entropy:

 

Example: log likelihood, cross-entropy, perplexity

 

5. Loss vs. performance

All these comparisons give us a measure of error of our model, that is how well our model corresponds to the real (true) phenomenon that we are modelling. We measure the error in different contexts for different purposes.

1. On the train set -> loss, training error for setting model parameters (weights)
2. On the dev set -> no standard term, but can be thought as interim performance, sometimes called validation, error measured for setting hyperparameters, e.g. the weight of a component in a processing pipeline, learning rate for weight updating, training duration etc.
3. On the test set -> performance, importantly, an estimate of the performance!

Only the last point is evaluation.

 

6. The baseline

When evaluating a NLP system, we want to know whether it performs better than another system. There is no point in reporting scores without a comparison. If no other system exists, then we compare our system to a simple solution, which does not involve learning. This simple solution is called the baseline. An example of such a simple solution is the majority class baseline – putting all test items in a single class, the one that is most frequently seen in the training set.

 

Common mistakes in evaluation

• “I get 78% accuracy - not bad!” » not bad compared to what?!
• “My system is not so good on the dev set, but it nails it on the test!” » your system got lucky with the test set
• “I’m happy with the accuracy, but I don’t like the F-score (so I’m not going to report it)” » there is probably one frequent label that your system gets well, but not the others

---